线性时间选择问题

元素选择问题(Select)：对于给定的包含n个元素的线性序集和一个整数k，1≤k≤n，找出这n个元素中第k小的元素。

1)基本思路：先排序(如：快速排序)，后查找。

2)改进思路：由于只需要查找第k小的元素，故只要递归查找划分后的某个分区即可，而无需全部排序。

元素选择问题的主程序

template<class Type>
Type RandomizedSelect(Type a[], int p, int r, int k)
{
      if (p==r) return a[p];
      int i=RandomizedPartition(a,p,r),
      j=i-p+1;
      if (k<=j) return RandomizedSelect(a,p,i,k);
      else return RandomizedSelect(a,i+1,r,k-j);
}

平均情况下需要O(n)计算时间。

最坏情况下需要O(n2)计算时间。

选择算法的改进(最坏情况为O(n))：如能在线性时间内找到一个划分基准，使得按这个基准所划分出的2个子数组的长度都至少为原数组长度的ε倍(0<ε<1，ε为正常数)，则可在最坏情况下用O(n)时间完成选择任务。

示例：

若ε=9/10，则算法递归调用所产生的子数组的长度至少缩短1/10。故在最坏情况下，算法所需的计算时间T(n)满足递归式：T(n)≤T(9n/10)+O(n) 。
由此可得T(n)=O(n)。

选择算法的改进：Select分治策略(查找满足要求的划分标准，假设所有元素互不相同)：

1)将n个元素划分成 $ \lceil n/5 \rceil $ 个组，每组5个元素，只可能有一个组不是5个元素。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共 $ \lceil n/5 \rceil $个。

2)递归调用Select来找出这 $ \lceil n/5 \rceil $个元素的中位数。如果 $ \lceil n/5 \rceil $ 是偶数，则找它的2个中位数中较大的元素作为划分基准。

选择算法的改进：Select分治策略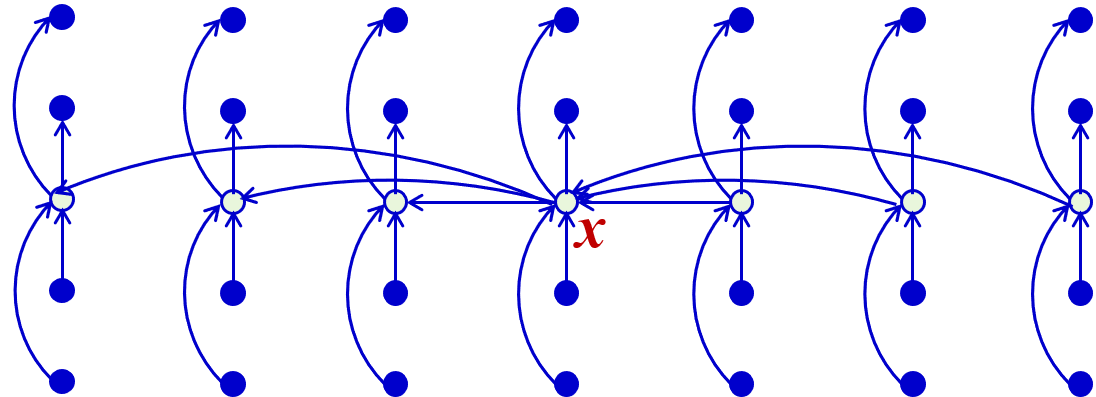

查找满足要求的划分标准的步骤如下（假设所有元素互不相同）：

1)这种情况下找出的基准x至少比3(n-5)/10个元素大，因为在每一组中有2个元素小于本组的中位数，而n/5个中位数中又有(n-5)/10个小于基准x。

2)同理，基准x也至少比3(n-5)/10个元素小。而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4。

改进的选择算法主函数Select

Type Select(Type a[], int p, int r, int k) //查找第k小的元素
{
      if (r-p<75) {
          用某个简单排序算法对数组a[p:r]排序; return a[p+k-1]; 
      };
      for ( int i = 0; i<=(r-p-4)/5; i++ ){
         将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      }
      Type x = Select(a, p, p+(r-p-4)/5, (r-p-4)/10); 
      //找中位数的中位数 (r-p-4即n-5) 
      int i=Partition(a, p, r, x),
      j=i-p+1;
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

改进的选择算法Select复杂性分析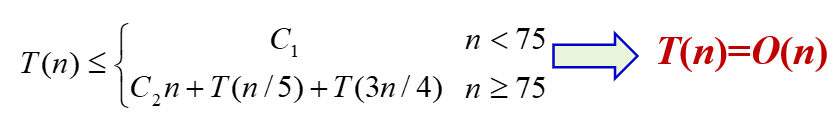

说明：

1)Select算法将每一组的大小定为5，并选取75作为是否递归调用的分界点。这2点保证了T(n) 递归式中的2个自变量之和n/5+3n/4=19n/20=εn，0<ε<1。这是使T(n)=O(n)的关键之处。

2)除了5和75之外，也可作其他选择。

实现：

/*
伪算法
Type Select(Type a[], int p, int r, int k) //查找第k小的元素
{
      if (r-p<75) {
          用某个简单排序算法对数组a[p:r]排序; return a[p+k-1];
      };
      for ( int i = 0; i<=(r-p-4)/5; i++ ){
         将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      }
      Type x = Select(a, p, p+(r-p-4)/5, (r-p-4)/10);
      //找中位数的中位数 (r-p-4即n-5)
      int i=Partition(a, p, r, x),
      j=i-p+1;
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

*/

#include <bits/stdc++.h>
using namespace std;

// 冒泡排序
void bubbleSort(int a[], int p, int r)
{
	for (int i = p; i < r; i++) {
		for (int j = i + 1; j <= r; j++)
			if (a[j] < a[i])swap(a[i], a[j]);
	}
}

// 按x划分，返回划分基准下标
int Partition(int a[], int p, int r, int x) {
	int i = p - 1, j = r + 1;
	while (true) {
		while (a[++i] < x && i < r);
		while (a[--j] > x && j > p);
		if (i >= j)
			break;
		swap(a[i], a[j]);
	}
	return j;
}

// p第一个数下标，r最后一个数下标，k要找的第k个数
int Select(int a[], int p, int r, int k) {
	// 规模小于75时直接排序查找
	if (r - p < 75) {
		bubbleSort(a, p, r);
		return a[p + k - 1];
	}
	// 分成n/5组，每组5个；找到每组中位数，放置队首
	for (int i = 0; i <= (r - p - 4) / 5; ++i) {
		// 将元素每5个分成一组，分别排序，并将该组中位数与a[p+i]交换位置，使所有中位数都排列在数组最左侧，以便进一步查找中位数的中位数
		// 将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
		bubbleSort(a, p + 5 * i, p + 5 * i + 4);
		swap(a[p + 5 * i + 2], a[p + i]);
	}
	int x = Select(a, p, p + (r - p - 4) / 5, (r - p - 4) / 10);
	//找到所有中位数的中位数 (r-p-4即n-5)
	int i = Partition(a, p, r, x);
	int j = i - p + 1;
	if (k <= j)
		return Select(a, p, i, k);
	else
		return Select(a, i + 1, r, k - j);
}

int main(int argc, char const *argv[])
{
	int x;
	//数组a存了0-79
	int a[80] = {3, 1, 7, 6, 5, 9, 8, 2, 0, 4, 13, 11, 17, 16, 15, 19, 18, 12, 10, 14, 23, 21, 27, 26, 25, 29, 28, 22, 20, 24, 33, 31, 37, 36, 35, 39, 38, 32, 30, 34, 43, 41, 47, 46, 45, 49, 48, 42, 40, 44, 53, 51, 57, 56, 55, 59, 58, 52, 50, 54, 63, 61, 67, 66, 65, 69, 68, 62, 60, 64, 73, 71, 77, 76, 75, 79, 78, 72, 70, 74,};
	cin >> x;
	printf("第%d大的数是%d\n", x, Select(a, 0, 79, x));

	return 0;
}