1076 Forwards on Weibo (30分)

发布日期: 2020-03-10

题意分析

给出每个用户关注的人，问如果给定的人发了一条微博，在所给的最大转发层数下，最多有多少个人会转发。注意给出的是每个用户关注的人，而不是关注该用户的人。

注意这道题用BFS很容易，用DFS也可以但容易出问题，后面将作详细分析。

广度优先遍历

定义一个level数组，表示每个用户转发时的当前转发层数，当转发层数到达给定的最大转发层数时，跳出循环。定义一个visit数组表示每个用户是否已经访问过，确保每个用户只被访问一次。然后利用广度优先遍历的算法进行搜索即可。

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 10;

vector<int>g[maxn];
int N, L;

int bfs(int u) {
	int ans = 0, level[N + 1] = {0}; //level表示用户转发时所处的转发层数
	bool vis[N + 1] = {false};
	queue<int>q;
	q.push(u);
	vis[u] = true;
	while (!q.empty()) {
		int t = q.front();
		q.pop();
		for (auto i : g[t]) {
			if (!vis[i] && level[t] < L) {
				ans++;
				level[i] = level[t] + 1;
				vis[i] = true;
				q.push(i);
			}
		}
	}
	return ans;
}

void addEdgr(int u, int v) {
	g[u].push_back(v);
}

int main(int argc, char const *argv[])
{
	cin >> N >> L;
	for (int u = 1; u <= N; ++u) {
		int M, v;
		cin >> M;
		for (int j = 0; j < M; ++j) {
			cin >> v;
			addEdgr(v, u);
		}
	}
	int K, id;
	cin >> K;
	for (int i = 0; i < K; ++i) {
		cin >> id;
		cout << bfs(id) << endl;

	}
	return 0;
}

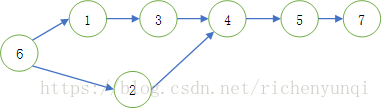
深度优先遍历

这道题使用深度优先遍历比使用广度优先遍历要复杂一些，原因在于对于一个在第 i 层访问到的用户来说，如果此时达到转发层数上限，就无法继续遍历了，然而如果该用户可以通过另一条更短的途径访问到，就可以继续深度遍历。比如样例输入：

如果转发层数上限为3，当6号用户发布微博时，先按6->3->1->4路径遍历，此时4号用户达到了转发层数上限，不再进行转发；但是按6->3->4->5的路径遍历，4号用户是可以继续遍历到5号的。但是如果先按第一条路径遍历的话，此时4号已经被访问过，当第二条路径到达4号用户时，不再继续进行遍历，这样的话就丢失了5号用户，使得答案错误。

那么怎么解决上述问题呢？一种方法是暴力搜索给定转发层数内所有的路径，允许同一个节点被访问多次，同时建立一个辅助数组visit，元素全都初始化为false，将路径经过的用户所对应的的数组中的元素置true，暴力搜索结束后，计算出visit内所有为true的元素个数-1即为所求（发布博客的用户本身不算转发，所以要减去1）。该算法的c++代码（为方便后面称呼，不妨叫做第一份代码）如下：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 10;

vector<int> g[maxn];
bool vis[maxn];

void dfs(int u, int level) {
	if (level < 0)
		return;
	vis[u] = true;
	for (int i = 0; i < g[u].size(); ++i) {
		dfs(g[u][i], level - 1);
	}
}

void addEdgr(int u, int v) {
	g[u].push_back(v);
}

int main(int argc, char const *argv[])
{
	int N, L;
	cin >> N >> L;
	for (int u = 1; u <= N; ++u) {
		int M, v;
		cin >> M;
		for (int j = 0; j < M; ++j) {
			cin >> v;
			addEdgr(v, u);
		}
	}
	int K, id;
	cin >> K;
	for (int i = 0; i < K; ++i) {
		cin >> id;
		memset(vis, false, sizeof(vis));
		dfs(id, L);
		cout << count(vis + 1, vis + N + 1, true) - 1 << endl;
	}

	return 0;
}

显然这种方法时间复杂度是非常高的，评测结果也说明了这一点：

测试点	结果	用时(ms)	内存(kB)	得分/满分
0	答案正确	2	384	18/18
1	答案正确	2	352	5/5
2	答案正确	1	364	2/2
3	答案正确	2	264	2/2
4	运行超时			0/3

那么有什么方法可以降低时间复杂度吗？我由样例想到了一种更好的算法，正如我前面所说的，先按6->3->1->4路径遍历时，4号用户已经被遍历过，造成了按6->3->4->5的路径遍历时无法从4号访问到5号。由此受到启发，我在前面所叙述的暴力搜索算法中做了一些修改，为了降低时间复杂度，仍要保证每个结点只能被访问一次，除了按某个路径遍历到的最后一个用户，以保证其他路径搜索到该用户时仍可以继续向下遍历，按样例来说就是当按6->3->1->4路径遍历到4时不把visit[4]置为true，使得按6->3->4->5的路径遍历时仍可以从4号访问到5号。各位对比着前面的第一份代码，看经过修改了的第二份c++代码应该更容易理解：

#include<bits/stdc++.h>
using namespace std;
int N,L,K;
vector<int> graph[1005];//图
bool visit[1005],person[1005];//visit表示是否已被访问，person用于最后统计
void DFS(int v,int level){
    person[v]=true;
    if(level==L)
        return;
    visit[v]=true;
    for(int i:graph[v])
        if(!visit[i])//保证每个用户只被访问一次，除了使得按某个路径遍历到的最后一个用户
            DFS(i,level+1);
}
int main(){
    scanf("%d%d",&N,&L);
    for(int i=1;i<=N;++i){
        int num,a;
        scanf("%d",&num);
        while(num--){
            scanf("%d",&a);
            graph[a].push_back(i);
        }
    }
    scanf("%d",&K);
    while(K--){
        fill(visit+1,visit+N+1,false);
        fill(person+1,person+N+1,false);
        int a;
        scanf("%d",&a);
        DFS(a,0);
        printf("%d\n",count(person+1,person+N+1,true)-1);
    }
    return 0;
}

评测结果为：

测试点	结果	用时(ms)	内存(kB)	得分/满分
0	答案正确	2	384	18/18
1	答案正确	2	352	5/5
2	答案正确	1	364	2/2
3	答案正确	2	264	2/2
4	答案正确	405	1000	0/3

完美的通过了所有的样例，但是刚才所说的算法就是正确的吗？我想到这样一组输入：

画成图形是这个样子：

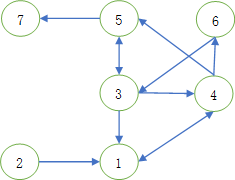
如果6号发布微博，转发层数上限为4层的话，大家可以依靠图形自行计算一下4层内能够遍历的用户个数，很明显是6，但是按照第二份代码，得出的结果却是5。我又使用广度优先遍历的代码测试了一下得出的结果依然是6。显然6是正确答案，那么第二份代码错在哪里呢？上面的输入有两条路径：6->1->3->4->5和6->2->4->5->7，在第二份代码的运行过程中先遍历的是6->1->3->4->5路径，此时1、3、4都被访问了一次，5虽然被访问了一次当后续再被访问时仍可继续向下遍历，但是1、3、4不可以。这样在遍历6->2->4->5->7路径访问到4这个节点时，就没有办法再向下遍历到5了，以至于最后只访问到1、 3、 4、 5、2这5个用户，所以得出了错误结果。究其原因，还是在于第二份代码只保证了每条路径的最后一个用户在被其他路径访问到时继续向下遍历，一旦其他路径遍历到的是不是最后一个用户而是其他用户，这个算法就会出错。但是pat给出的测试点中没有测试这个点，所以第二份代码虽然是错误的代码，仍通过了所有测试用例。

那么有没有正确的代码呢？我又思考了一下，发现可以这样，为了避免上述问题，每个结点不可避免的要被多次访问，但是又要设置某些限制条件进行剪枝，那么遍历的条件可以这样设置：借鉴于广度优先遍历的方法，可以设置一个数组layer存储每个结点被遍历到时的层数，每个结点要想继续进行深度优先遍历，要么这个节点以前从未访问过，要么这个节点当前被访问时的层数小于layer数组中对应的层数，整个第三份c++代码如下所示：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 10;

vector<int> g[maxn];
bool vis[maxn];  //vis表示是否已经被访问
int layer[maxn];  //储存每个结点被遍历到时的层数
int N, L;

void dfs(int u, int level) {
	if (level == L + 1)
		return;
	vis[u] = true;  //当前结点置为已访问
	layer[u] = level; //更新被遍历时所处层数
	for (auto i : g[u]) {
		if (!vis[i] || layer[i] > level + 1) { //这个节点以前从未访问过或者这个节点当前被访问时的层数<layer数组中对应的层数
			dfs(i, level + 1);
		}
	}
}

void addEdgr(int u, int v) {
	g[u].push_back(v);
}

int main(int argc, char const *argv[])
{
	cin >> N >> L;
	for (int u = 1; u <= N; ++u) {
		int M, v;
		cin >> M;
		for (int j = 0; j < M; ++j) {
			cin >> v;
			addEdgr(v, u);
		}
	}
	int K, id, ans;
	cin >> K;
	for (int i = 0; i < K; ++i) {
		cin >> id;
		memset(vis, false, sizeof(vis));
		memset(vis, -1, sizeof(layer));
		ans = 0;
		dfs(id, 0);
		for (int i = 1; i <= N ; ++i)  //遍历layer数组，元素>0的即为符合条件的人，进行递增
			ans += layer[i] > 0 ? 1 : 0;
		cout << ans << endl;
	}

	return 0;
}